There are a number of ways to use the subtraction formula in Excel. It not just saves plenty of time but also makes you productive at the professional front. If you regularly use Excel then you might be aware of its subtraction formula. However, there are a few ones that find the subtraction formula complicated in an Excel sheet. If you are one of them, here you can learn how to create a subtraction formula in Excel 2010 or 2013. This way, you can easily apply the subtraction formula in Excel even if you are a beginner for using an Excel sheet.
The tutorial focuses on the following subtraction formulas:
- Basic subtraction formula in Excel
- Formula to subtract numbers in Excel
- Subtract cells in Excel
- Subtract multiple cells from one cell
- Subtract column in Excel
- Subtract the same number from a column of numbers
- Date subtraction in Excel formula
- Formula to subtract time in Excel
- Formula for subtracting percentage in Excel
What is the Subtraction Formula in Excel?
The subtraction function does not exist in Excel. However, you can use the basic subtraction formula which is a minus sign (-). For instance, you want to subtract 1 from 10, you can write the equation =10-1 and get 9 as a result. Below are the following steps on how to subtract in excel formula.
Step 1: To enter the subtraction formula in Excel, you can type the equality sign (=) in a cell (where you want the result to display).
Step 2: Then, you can enter the first number with a minus sign.
Step 3: After that, you can enter the second number which should be subtracted with the first number.
Step 4: As the last step, you can hit the Enter key to complete the formula.
Apart from that, you can perform more than one arithmetic operation within a single formula. For instance, to subtract multiple numbers from 100, you can type those numbers separated by a minus sign as shown below.
=100-20-30
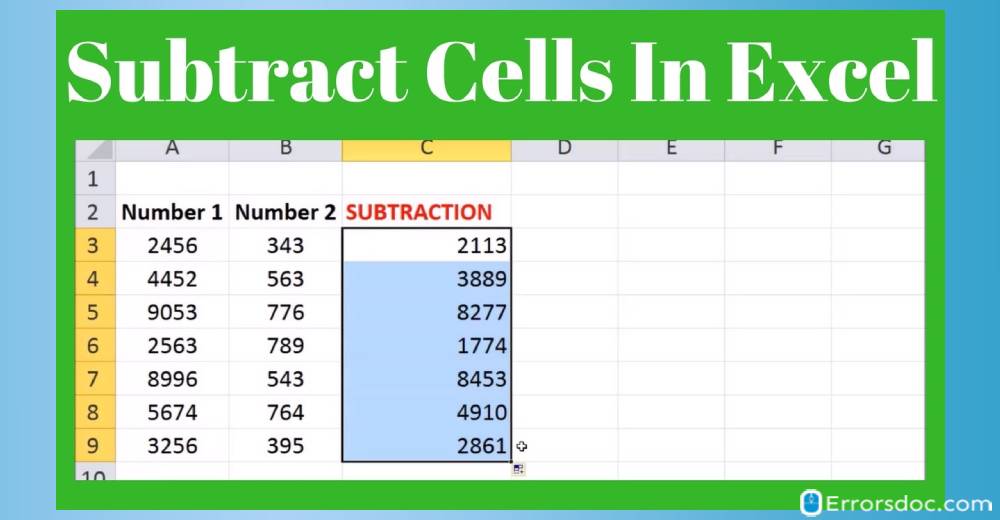
How to Subtract Cells in Excel?
In Excel, you can also subtract one cell from another using the minus formula. But, in this case, you need to supply cells instead of the numbers. It should be something as shown below.
=cell_1 – cell_2
If you want to subtract the figure in B2 from the figure in A2, you can use this formula (=A2-B2).
However, it is not necessary to type cell references manually. Instead of this, you can add them to the formula by picking the corresponding cells. To do so, you can go through the steps mentioned below.
Step 1: To begin, type the equals sign (=) in a cell where you want the output to appear.
Step 2: Now, you can click on the cell that contains a minuend (a quantity from which another number needs to be subtracted). Doing so, the reference will be added to the formula (A2) automatically.
Step 3: Thereafter, you can enter the minus sign (-).
Step 4: Once done, click on the cell that contains a subtrahend (a quantity to be subtracted) in order to add its reference to the formula (B2).
Step 5: As the last step, hit the Enter button to complete your formula.
How to Subtract Multiple Cells from One Single Cell in Excel?
To subtract multiple cells from only one cell, multiple methods can be performed. You can try the following three kinds of methods.
Method 1: Use Minus Sign
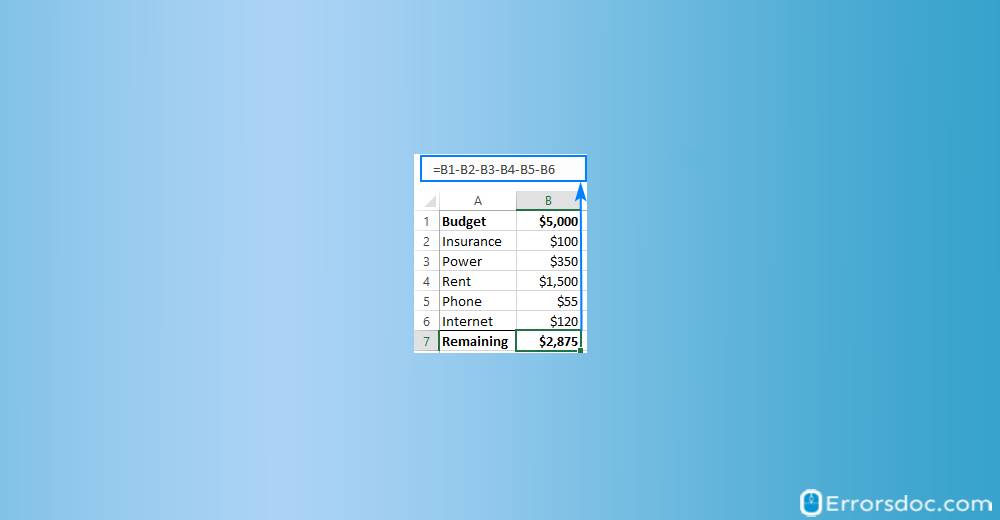
The first way to use the subtraction formula in Excel is simple for subtracting multiple cells from one cell. All you need to type cell references separated by a minus (-). For example, to subtract cells B2: B5 from B1, you can create a formula as shown down below.
=B1-B2-B3-B4-B5
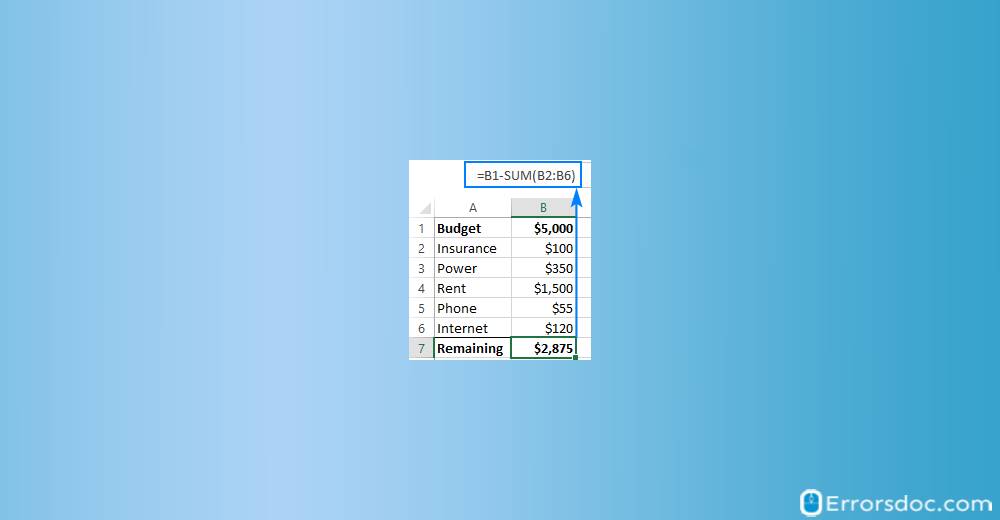
Method 2: Use the SUM Function
To make a compact formula, you can add up the subtrahends (B2 : B5) with the help of the SUM function. Then, you can easily subtract the sum from the minuend (B1).
=B1 – SUM (B2 : B5)
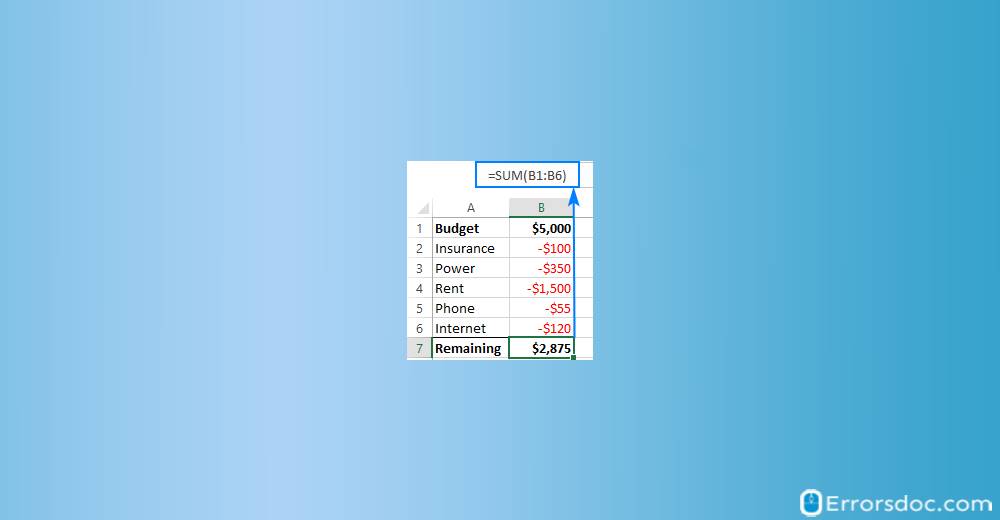
Method 3: Sum Negative Numbers
Since subtracting the negative numbers is the same as adding a number so you need to make all the numbers that you want to subtract negative. To do so, you can type a minus sign before a number. Then, you can use the SUM function in order to add negative numbers. See below.
=SUM (B1 : B5)
How to Put a Subtraction Formula in Excel for Columns?
To subtract two columns row by row, you can simply write a minus formula for the topmost cell. Then, you can double click the plus sign or drag the fill handle to copy the formula to the whole column.
For example, to subtract numbers in column B from the numbers in column A, start with row 2. See below to get the example.
=A2-B2
Because of the use of relative cell references, the formula will adjust properly from each row.
How to Subtract the Same Number from a Column of Numbers?
To subtract one number from a range of cells, you can enter the number in a cell and subtract the cell from the first cell in the range. Suppose you take F1 so the formula will be like as shown below
=B2-$F$1
The important key is to lock the reference for the cell that needs to be subtracted with $ sign. Doing so will create the absolute cell reference that does not change (no matter where the formula is copied). The first reference (B2) is not locked so it can change for each row.
Consequently, in cell 3, you will have the formula as shown below.
=B3-$F$1
Whereas, in cell 4, the formula will change to (=B4-$F$1) and so on.
How to Subtract Date in Excel Formula?
The easiest way to subtract dates in an Excel sheet is to enter dates in individual cells and then subtract one cell from another.
=End_date – Start_date
Apart from this, you can supply dates directly in your formula using the DATE or DATEVALUE function. For example:
=DATE (2019,2,1) – DATE (2019,1,1)
=DATEVALUE (‘2/1/2019’) – DATEVALUE (“1/1/2019)
How to Subtract Formula in Excel for Time?
The formula for subtracting the time in the Excel sheet is similar to the date formula.
=End_time – Start_time
If you want to get the contrast between the times in A2 and B2 then you can use the formula mentioned below.
=A2-B2
To get the correct output, make sure that you are applying the Time format to the formula cell. You can get the same result if you supply the time values directly in the formula. To understand the time correctly in Excel, use the TIME VALUE function as shown below.
=TIMEVALUE (‘4:00 PM”) – TIMEVALUE (“12:00 PM”)
What is the Formula for Subtracting Percentage in Excel?
If you want to learn how to write subtraction formula in Excel for percentages then you can use the following ideas.
To subtract one percentage from the other, the familiar minus formula will work. For example: (=100% – 40%)
Or, you can also enter the percentages in cells individually in order to subtract those cells such as (=A2-B2)
If you want to add a subtraction formula in Excel from a number (decrease number by percentage) then you can use the formula mentioned below.
=Number * (1-%)
Here is how to reduce the number in A2 by 20%.
=A2* (1-20%)
Besides that, you can enter the percentage in an individual cell (B2) and refer to the cell by using the absolute reference.
=A2* (1-$B$2)
Conclusion
If you were finding a clear guide on how to do a subtraction formula in Excel then the above-mentioned methods or techniques will enlighten you. It covers different ways to use the subtraction formula in Excel sheets with ease.